Statistische Lerntheorie und Empirische Inferenz
Forschungsbericht (importiert) 2003 - Cyberneum
Lernen aus Beispielen
Das Problem des Lernens aus Beispielen [7] lässt sich wie folgt formulieren: sei y = f(x) ein unbekannter funktionaler Zusammenhang der Größen x und y. Ziel ist, aus einer begrenzten Anzahl von Beispielen (der Trainingsmenge) (x1,y1),…, (xl,yl) die Funktion f zu lernen.
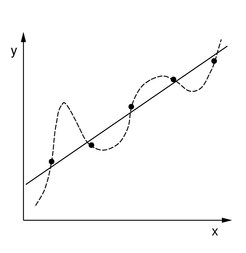
Welche Aspekte gilt es hierbei zu berücksichtigen, um zu einer verlässlichen Schätzung f* zu kommen? Zunächst einmal sollte die gelernte Funktion die Beispiele erklären, d.h. f*(x1) = y1,…,f*(xl) = yl, wenigstens näherungsweise. Abbildung 1 zeigt, dass dies noch nicht alles ist: Die abgebildeten Beispiele werden durch die gestrichelte Funktion im Gegensatz zu der durchgezogenen Geraden vollständig erklärt; nichtsdestotrotz ist man geneigt, der Geraden mehr Vertrauen zu schenken. Die Komplexität der (Klasse von) Funktionen, die man für die Lösung des Problems zulässt, beeinflusst also unser Vertrauen in die gefundene Lösung. Die Formalisierung dieser Erkenntnis bildet den Kern der statistischen Lerntheorie.
Der Einfachheit halber werden wir uns im folgenden auf (binäre) Mustererkennung beschränken, d.h. auf Funktionen, die nur zwei verschiedene Werte annehmen können (so genannte Entscheidungsfunktionen). Obige Erkenntnis von der Wichtigkeit der zugelassenen Funktionen berücksichtigen wir, indem wir das Lernproblem wie folgt fassen:
Gegeben sei eine Menge von Entscheidungsfunktionen, und eine Menge von Trainingsbeispielen (x1,y1),…, (xl,yl), zufällig erzeugt gemäß einer unbekannten Wahrscheinlichkeitsverteilung. Ziel ist es, eine Funktion auszuwählen, die den Zusammenhang zwischen x und y für Testbeispiele, gezogen aus derselben Wahrscheinlichkeitsverteilung, am besten wiedergibt.
Die Muster x könnten z.B. Repräsentationen von Krankheitssymptomen sein, aus denen auf das Vorhandensein y einer bestimmten Krankheit geschlossen werden soll. Der Zusammenhang zwischen x und y wird durch eine Wahrscheinlichkeitsverteilung P(x,y) modelliert. Diese enthält als Spezialfall die Möglichkeit eines deterministischen Zusammenhanges y = f(x).
Die gesuchte Funktion soll den Zusammenhang zwischen x und y im Mittel am besten reproduzieren (die Wahrscheinlichkeit für Klassifikationsfehler bei Testbeispielen, das (erwartete) Risiko, soll minimal sein). Die Mittelung wird hierbei gemäß der Wahrscheinlichkeitsverteilung P(x,y) vollzogen. Da man diese nicht kennt, benötigt man ein Induktionsprinzip, um die Funktion wenigstens näherungsweise zu finden, und zwar auf Basis dessen, was wir über P(x,y) beobachtet haben, also der Trainingsmenge.
Induktionsprinzipien
Eine nahe liegende und vielfach verwendete Methode zur Risikominimierung besteht in der Minimierung des empirischen Risikos, also des Anteils der Fehlklassifikationen auf der Trainingsmenge. Das Prinzip der empirischen Risikominimierung ist jedoch kein Garant für hohe Generalisierungsfähigkeit: Ein nicht in der Trainingsmenge enthaltenes Beispiel, erzeugt gemäß derselben Wahrscheinlichkeitsverteilung, liegt nicht notwendig auf der gestrichelten Linie in Abbildung 1. In anderen Worten: Von einem niedrigen empirischen Risiko alleine kann nicht auf ein niedriges erwartetes Risiko geschlossen werden. Hierzu muss gleichzeitig die Kapazität der Funktionsklasse kontrolliert werden, die sich beispielsweise durch die Vapnik-Chervonenkis-(VC-)Dimension messen lässt. Der trade-off zwischen Minimierung des empirischen Risikos und der Kapazität wird durch probabilistische Schranken beschrieben, deren Studium ein wesentliches Thema der Lerntheorie ist.
Die anschauliche Bedeutung dieser Schranken lässt sich wie folgt fassen: Schafft man es, die Trainingsdaten mit einem einfachen Modell (d.h. einer Funktionsklasse, deren VC-Dimension im Vergleich zur Anzahl der Trainingsbeispiele niedrig ist) zu erklären (d.h. das empirische Risiko gering zu halten), so besteht Grund zu der Annahme, dass der wirkliche funktionale Zusammenhang gefunden wurde. Kann man die Daten nur mit einer Lernmaschine (bzw. Funktionsklasse) von vergleichsweise hoher VC-Dimension erklären, so ist dies nicht der Fall: Die Maschine kann ihre Kapazität (VC-Dimension) dazu verwendet haben, die Beispiele einzeln zu memorisieren (overfitting), anstatt eine kompaktere zugrunde liegende Regularität zu lernen — dementsprechend ist nicht zu erwarten, dass neue Beispiele zuverlässig klassifiziert werden können. Das Prinzip der strukturellen Risikominimierung verwendet oben genannte probabilistische Schranken, um das erwartete Risiko durch Kontrolle von empirischem Risiko und VC-Dimension zu minimieren, d.h. um eine Funktion zu finden, die möglichst gut auf neue Beispiele generalisiert. Strukturelle Risikominimierung passt also in diesem Sinne die Komplexität der Lernmaschine dem zu lösenden Problem an, und stellt somit eine Basis für moderne Lernalgorithmen dar.
Die VC-Dimension stimmt in manchen Fällen mit der Anzahl der Parameter einer Funktionsklasse überein, die wiederum oft mit der Dimensionalität der Beobachtungsgrößen xi zusammenhängt. So lässt sich verstehen, dass die Anzahl der freien Parameter manchmal als ein Maß für die Komplexität oder Kapazität einer Funktionsklasse betrachtet wird. Dies ist allerdings nicht immer richtig, mit der nachteiligen Konsequenz, dass die Abschätzung der Komplexität einer Funktionsklasse sich nicht auf das Zählen von Parametern reduziert, sondern ein schwieriges mathematisches Problem sein kann. Der Vorteil ist jedoch, dass die Hoffnung besteht, auch dann noch generalisieren zu können, wenn die Daten (bzw. die Parametervektoren) sehr hochdimensional sind. Eine Klasse von Lernalgorithmen, die diese Hoffnung bestätigen, wurde in den letzten Jahren als Support-Vektor-Maschinen (SVM) oder allgemeiner Kernalgorithmen bekannt [5, 6].
Kernalgorithmen
Die Schwierigkeit beim Abschätzen der Kapazität von Funktionsklassen besteht darin, dass Größen wie die VC-Dimension kombinatorischer Natur sind. Dies führt zu einem Dilemma: Gute Abschätzungen existieren vor allem für einfache (z.B. lineare) Funktionsklassen; Auf der anderen Seite ist es aber unser Ziel, Lernalgorithmen zu konstruieren, die für nichtlineare Funktionsklassen funktionieren. Nur so können wir hoffen, damit komplexe Phänomene der Naturwissenschaften analysieren zu können. Dieses Dilemma wird von Kernalgorithmen elegant aufgelöst. Die von Kernalgorithmen verwendeten Funktionen entsprechen linearen Funktionen in einem zugeordneten hochdimensionalen Merkmalsraum H; als Funktionen auf den Eingabedaten sind sie jedoch nichtlinear. Die theoretische Analyse kann in dem Merkmalsraum vorgenommen werden, in der Praxis arbeiten wir aber mit nichtlinearen Funktionen.
Im Fall der Mustererkennung tun Support-Vektor-Maschinen dies, indem sie die Muster effektiv in einen hochdimensionalen Merkmalsraum abbilden und dort eine Hyperebene zur Separation der beiden Klassen konstruieren. Für diese Funktionsklasse lässt sich die VC-Dimension abschätzen und algorithmisch kontrollieren. Durch Lösung eines quadratischen Optimierungsproblems findet man die Funktion, die die beste Generalisierungsleistung verspricht. Es stellt sich heraus, dass diese Funktion nur von wenigen Trainingsbeispielen, den Support-Vektoren, abhängt. Klassifikation eines neuen Musters geschieht durch gewichteten Vergleich mit den Support-Vektoren. Unterschiedliche Typen von Support-Vektor-Maschinen lassen sich durch die Wahl des so genannten Kernes k implementieren. Allen Kernalgorithmen ist gemein, dass der Kern ein Skalarprodukt im Merkmalsraum H berechnet. Formell bedeutet dies, dass eine Abbildung Φ : χ → H existiert mit der Eigenschaft, dass für alle Eingabedaten x,x' welche Elemente aus χ sind die Gleichung k(x,x') = ‹Φ(x),Φ(x')› gilt. Beispiele von solchen positiv definiten Kernen sind, unter geeigneten Bedingungen an den Inputraum χ, der Gauß-Kern k(x,x') = exp(-||x - x'||2) sowie der Polynom-Kern k(x,x') = ‹x,x'›d (wobei d Elemente aus der Menge der natürlichen Zahlen sind). Man kann zeigen, dass letzterer eine Abbildung Φ induziert, die alle Produkte der Ordnung d in den Inputkoordinaten berechnet.

Positiv definite Kerne lassen sich auch für Datentypen definieren, die nicht vektorieller Natur sind, wie z.B. Sequenzdaten. Die Abbildung Φ liefert dann eine Repräsentation der Daten in dem Skalarproduktraum H — so können geometrische Methoden für allgemeine Datentypen verwendet werden. Dies hat zu einer Reihe von interessanten Anwendungen insbesondere im Bereich der computational biology geführt [6, 3]. Aber auch in anderen Feldern sind mit Kernmethoden sehr gute Ergebnisse erzielt worden, so zum Beispiel in der Objekterkennung und -Detektion [4], und im Training von Brain-Computer-Interfaces [2]. Besonders attraktiv an Kernmethoden ist aber nicht nur die Tatsache, dass die Anwendungsergebnisse hervorragend sind und Weltrekorde auf bekannten Benchmarks einschließen [1, 8], sondern, dass sie drei Grundprobleme der empirischen Inferenz thematisieren:
• Datenrepräsentation — der Kern k induziert eine Einbettung der Daten in den Vektorraum H
• Ähnlichkeit — der Kern k kann als (nichtlineares) Ähnlichkeitsmaß aufgefasst werden, mit dem Datenpunkte verglichen werden
• A-priori-Wissen — die Lösungen von Kern-Lernalgorithmen lassen sich im Allgemeinen als Kern-Entwicklungen in den Trainingsdaten ausdrücken. Daher parametrisiert der Kern die Klasse der Funktionen, aus denen die Lösung entnommen wird, d.h., dasjenige Wissen, das zusätzlich zu den Trainingsdaten in den Lernprozess eingeht.
Schlussbemerkung
Methoden des maschinellen Lernens wurden entwickelt zur Lösung von Induktionsproblemen, wie sie in den Naturwissenschaften überall vorkommen. Der traditionelle Ansatz zur Lösung solcher Probleme besteht darin, ein vorliegendes System so detailliert zu studieren, bis die zugrunde liegenden Vorgänge aufgedeckt sind und ein mechanistisches Modell aufgestellt werden kann. Das maschinelle Lernen kann solche Modelle nicht liefern, ist aber dafür in vielen Fällen einsetzbar, wo mechanistische Modelle nicht möglich sind, weil die zugrunde liegenden Prozesse zu komplex sind. Falls Trainingsdaten vorliegen, kann es uns in solchen Fällen oft zu sehr guten Nachbildungen von interessanten Aspekten komplexer Systeme liefern, die deren Verständnis entscheidend voranbringen können. Moderne Methoden des maschinellen Lernens und der empirischen Inferenz werden eine wesentliche Rolle beim Umgang mit einer komplexen Welt spielen.

